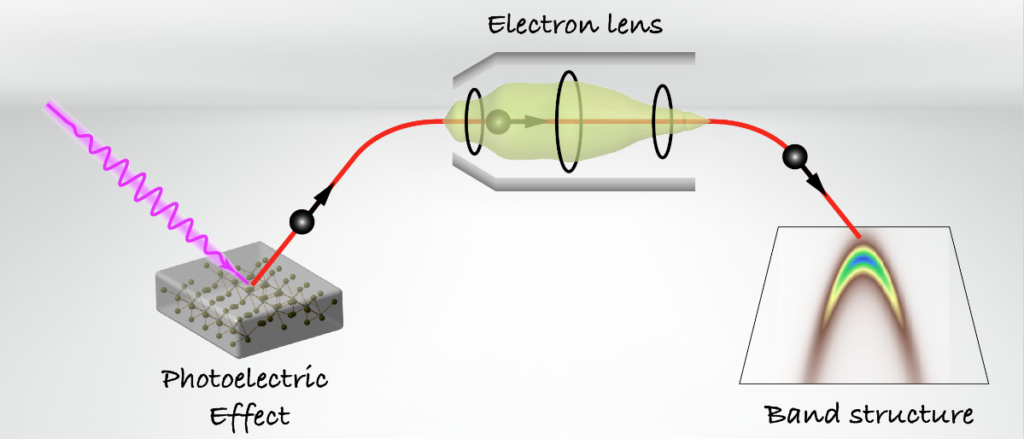
Angle-Resolved Photoelectron Spectroscopy (ARPES) is a useful tool to probe electronic structures of crystals. Based on photoelectric effect, we use a light to kick out the electrons, and measure the angle (k) and energy (E) of outgoing photoelectrons. The photoelectron intensity can be expressed as \(I(k,E) \sim M A(k,E) f(E)\).

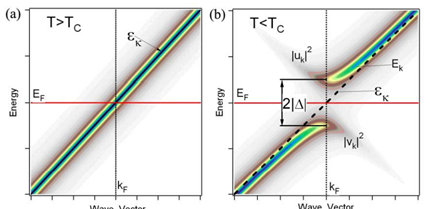
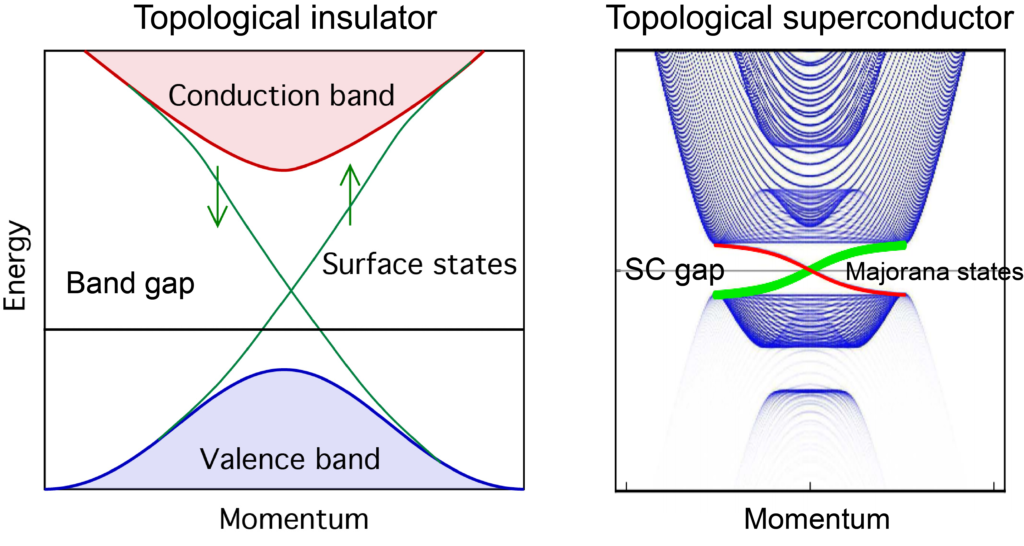
Band dispersion is directly contained in the spectral function \(A(k,\omega)\). Thus, any physical problem, that is related to band dispersion, can be studied by ARPES. Some examples are: Topological materials with special band structure; Superconductors: Gap opening in the band dispersion will appear at Fermi level in the superconducting state; Nematic order: Band degeneracy at high symmetry points will be lifted due to the symmetry breaking; Electron-phonon coupling: A kink structure will appear in the band dispersion at the phoono energy; and so on. All these phenomenons are related to the band dispersion, which can be readily studied by ARPES.

We also need to be aware of the spectral weight in the spectral function \(A(k,E)\). In most cases, we are only interested in the band dispersion, and ignore the spectral weight. However, the spectral weight of a band may not be the same over entire Brillouine zone, which may change the appearance of a band in ARPES. In a superconductor, the band dispersion is particle-hole symmetric. But in the spectral function, only part of the band is shown, since the electron weight is not one for all the states. The impurity state is another example. We expect a non-dispersive band for impurity states as the impurities have no translation symmetry. However, in the spectral function, we find that the impurity states are highly localized in momentum space, and only a small part of the non-dispersive band is occupied. ¹

The matrix element effect \(M\) is related to many factors such as the symmetries of electron orbitals in solids, the polarization of light, and photon energies. It is usually complicated and cannot be fully understood in most of the cases. However, the ARPES setup generally has mirror symmetries. From the mirror symmetry eigenvalues of \(\psi_f\), \(\mathbf{P}\) and \(\psi_i\) in \(M \sim <\psi_f|\mathbf{A} \cdot \mathbf{P}|\psi_i>\), we can get information on the orbital character of the bands. ²

Superconductivity is a crucial properties of certain materials which characterized by zero-resistivity and Meissner effect. Below the critical temperature T_C, the resistivity will drop to zero abruptly, and inside the superconductor satisfies B=0 regardless of the existence of external magnetic field H. These two properties are essential in observation of superconductivity, and have many important applications such as the superconducting maglev train, superconducting coils, and so on.

In general, superconductors can be divided into conventional superconductors and unconventional superconductors. Conventional superconductors consist of the most metals, compounds and alloys, and it can be interpreted by the BCS theory successfully, which is presented by J. Bardeen, L. Cooper and J. R. Schrieffer in 1957, and they won the Nobel Prize in physics in 1972 for this theory. Based on the assumption of weak coupling, it claims that superconductivity is a novel state of electrons and protected by the superconducting gap \(2\Delta\). In the framework of BCS theory, the superconductivity is a macroscopic quantum coherent effect and arises from the condensation of Cooper pairs. Around the Fermi Surface, the BCS theory argues that with the participation of phonons the electrons with opposite momentum vector (k, -k) will form Cooper pairs. The BCS theory gives a profound understanding of superconductivity, and in great agreement with most experiments.

However, BCS theory cannot explain the unconventional superconductors perfectly. Some novel pairing mechanisms beyond electron-phonon coupling and the strong correlation effect of electrons have been proposed. In 1986, Bednorz and M\(\ddot{u}\)ller found the cooper oxide superconductor, and its critical temperature is about 30 K，after that more and more cooper-based superconductors have been discovered and their critical temperature is higher than McMillan limitation in BCS theory. Nevertheless, in 2006 the Japanese group discovered the first iron-based superconductor, and they have some similar properties as cooper-based superconductors. In general, the high-temperature superconductors have layered structure such as the CuO₂ planes in cooper-based superconductors and FeAs or FeSe planes in iron-based superconductors, which is crucial for the existence of superconductivity. Currently, there is not a unified interpretation of high-temperature superconductors. Because of the extraordinary ability of detecting energy dispersions, ARPES is a powerful tool to study high-temperature superconductors.

The electronic structures of topological materials have a property which is invariant under some topological continuous deformation. Topological materials consists of various types such as topological insulators, topological semimetals, topological superconductors and so on.

Topological insulators are materials with conducting surface states and insulating bulk states. Backscattering of the surface states by nonmagnetic impurities is prohibited, which may lead to wide applications in spin engineering. The most definite evidence of topological insulators is the existence of spin-polarized Dirac-bands at the surfaces. In contrast, topological semimetals, such as Dirac semimetals, Weyl semimetals, topological nodal-line semimetals, host Dirac bands in the bulk. Topological semimetals have some interesting properties, such as Fermi arc states, monopoles of Berry curvature in momentum space, resulting in unique electric transports.

When the electronic structure of superconducting Bogoliubov quasiparticles is topological, the material is a topological superconductor. There are Majorana states at the surface/edge of a topological superconductor, which satisfy non-abelian statistics. It is proposed that the proximity effect between a topological insulator and an s-wave superconductor can produce topological superconductivity at the interface. This proposal can be realized in a heterostructure of a topological insulator and an s-wave superconductor. In iron-based superconductors, the topological insulator state and the superconducting state coexist in a single crystal, which is much easier to fabricate and study than a heterostructure. Iron-based superconductors provide a simple and high-Tc platform to study topological superconductors.